Um das Verhalten des vorgestellten Modells zu untersuchen und die Wirkung des Rückstaus auf die Wegewahl zu zeigen, wird hier ein einfaches Beispiel analysiert. Das Beispiel wird mit Visum ausgeliefert und liegt im Unterverzeichnis DUE als Braess_without_spillback.ver und Braess_with_spillback.ver im Ordner Training.
Folgendes bezieht sich auf das in Abbildung 133 dargestellte Braess-Netz. Strecken haben die in der Tabelle aufgeführten Eigenschaften und werden alle mit einem parabolischen Fundamentaldiagramm modelliert. Alle Streckenausgangskapazitäten werden den entsprechenden Eingangskapazitäten gleichgesetzt. Die Abbiegekapazitäten sind QAC = QAE = QED = 2 000 Fzg/h und QBD = QCF = QDF = 1 000 Fzg/h.
|
Strecke |
La[km] |
Qa [Fzg/h] |
Va [km/h] |
Wa [km/h] |
1 / Ka[m] |
|
A |
0,4 |
2 000 |
50 |
15 |
7,0 |
|
B |
0,6 |
2 000 |
50 |
15 |
7,0 |
|
C |
0,6 |
2 000 |
50 |
15 |
7,0 |
|
D |
0,4 |
2 000 |
50 |
15 |
7,0 |
|
E |
0,4 |
2 000 |
50 |
15 |
7,0 |
|
F |
0,1 |
4 000 |
50 |
15 |
3,5 |
Der Umlegungszeitraum besteht aus 100 Intervallen von je 1 Minute. Es wird von einer konstanten Nachfrage für die ersten 33 Simulationsminuten von Knoten 1 zu Knoten 5 ausgegangen, was D15 = 2 300 Fzg/h entspricht.
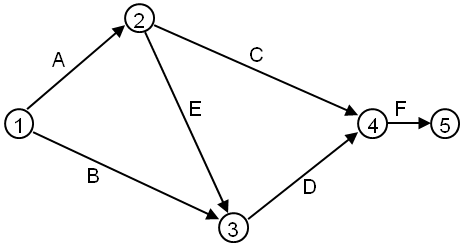
Abbildung 133: Das Beispielnetz
Die Ergebnisse von zwei Umlegungsläufen, einer mit und einer ohne Rückstauberechnung, werden in Abbildung 134 dargestellt. Ohne Rückstau sind nur die Abbieger CF und DF überlastet, und zwar zu gleichen Teilen (was den Fahrzeiten entnommen werden kann), sodass auf allen Wegen zwischen Knoten 1 und Knoten 5 die Warteschlangen gleich sind und Weg A-E-D-F weniger befahren wird, da er ungünstiger ist. Mit Rückstau wird der Stau jedoch von Abbieger CF auf Kante C und weiter bis hin zur Kante A propagiert, ebenso von Abbieger DF auf Kante D und weiter bis zu den Kanten B und E. Außerdem ist der Rückstaueffekt auf Kante B wegen der unterschiedlichen Kapazitäten von Abbieger ED und Abbieger BD größer als auf Kante E. Nach dem anfänglichen Anstieg bleibt die Fahrzeit auf Kante D dann konstant, da der Stau aufwärts propagiert wird, während die Fahrzeit auf Kante B schneller ansteigt als die Fahrzeit auf der Kante E, sodass der Weg A-E-D nun attraktiv wird, da er zwar einen längeren Weg, aber eine kürzere Fahrzeit bedeutet. Deshalb steigt die Belastung auf Kante E von etwa 150 Fzg/h auf 670 Fzg/h an.
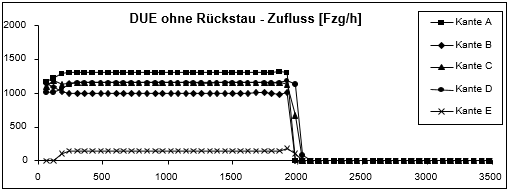
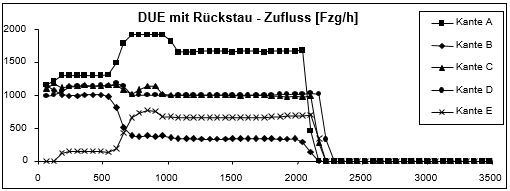
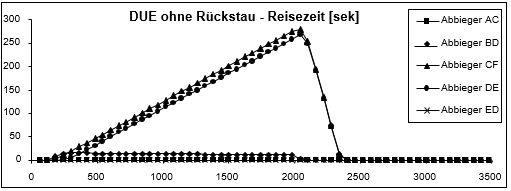
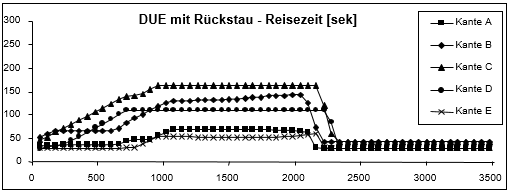
Abbildung 134: Ergebnisse der Dynamischen Gleichgewichtsumlegung mit und ohne Rückstauberechnung

